Snakes and Ladders (Part 2 of 3): Analysing the classic children’s game

In the previous post in this series, we set out the basic Python code required to simulate a single game of snakes and ladders. In order to analyse the game in more detail we will be required to simulate multiple random games so that we can look at certain properties, such as expected game lengths, the occupancy of squares, and the advantage to playing first. We tackle the latter of these in what follows.

The main change we make to our existing code is to wrap the initialisation of starting squares and the infinite loop in an outer for loop. This will allow us to iterate as many times as we choose. Here we have selected 1,000,000 to keep run times to a reasonable level.

In addition to this we will also require two new variables to count the number of wins per player. Finally, note also that we have included a random seed for reproducibility.

The updated code is now:

import numpy as np


def snakes_and_ladders(x):
    dict_sal = {21:3, 24:7, 35:9, 50:11, 53:15, 60:23,
                75:44, 89:48, 93:25, 97:65, 99:58,
                4:16, 12:33, 18:22, 26:37, 42:61,
                49:51, 55:74, 82:98, 85:95, 88:92}
    return dict_sal.get(x, x)

def roll_die(x):
    x += np.random.randint(1, 7)
    x = snakes_and_ladders(x)
    return x

p1_wins = p2_wins = 0

np.random.seed(42)

NUM_GAMES = 1000000

for game in range(NUM_GAMES):
    p1 = p2 = 0
    while True:
        p1 = roll_die(p1)
        if p1 >= 100:
            p1_wins += 1
            break
        p2 = roll_die(p2)
        if p2 >= 100:
            break

print p1_wins, p2_wins

The above code is available here.

Running this code yields a total of 505,845 wins for P1, and 494,155 wins for P2. To me this is quite an unexpected result, since the benefits of moving first are very marginal (50.6% versus 49.4%).

For comparison with a straight race to 100 we can simply comment out the line x = snakes_and_ladders(x). On doing so the win percentages shift to 55.3% versus 44.7% for Players 1 and 2 respectively. This shows that the inclusion of snakes and ladders in the game is a very effective equaliser against the first roll advantage.

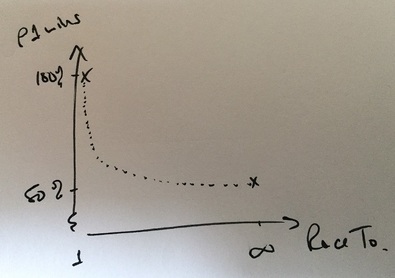
One interesting observation on this, made by a good friend of mine William Hanbury, is that the snakes and ladders board can theoretically be replicated by a straight race to n, for some specific value of n. To see this imagine that n is very small. Then in some cases (n <= 6) Player 1 will win before Player 2 has even had a chance to roll. Consequently, Player 1’s win percentage will be very high (if n = 1 then P1 always wins, or using n = 5 for example gives percentages of 69.1% against 30.9%).

We already have that with n = 100 the percentages are 55.3% and 44.7%, whilst in the limit as n goes to infinity they will approach 50% each. Therefore at some point between 100 and infinity there exists an n such that the win rates match those above simulating the actual snakes and ladders game. What this number is remains an open question, but it is undoubtedly very large indeed.

In the final post in this series we produce some visual results, showing the distributions of game lengths and the frequency with which the various squares are landed on.